Introduction
Superposition of folding can lead to very complex layer geometries, which when observed in 2D (e.g. outcrop) are called interference patterns. Commonly used names for the different patterns are 'crescent', 'mushroom', 'hook', 'bird's head', dog's tooth' and 'S-Z-W-M' shapes. Many Structural Geology textbooks illustrate idealised patterns either as 2D sections or as block diagrams. Computer programs and animations are also available that provide 2D and 3D visualisation of refolded folds. However, students (and teachers, including myself) often find it difficult to visualise these complex geometries in 3D. Here we provide a range of papermodels of superposed folds that hopefully will help students to improve their ability to infer the 3D geometry from 2D sections. Because drawing interference patterns is by no means trivial I have written a Matlab script which can be downloaded for free and with which users can create their own papermodels.
The purpose of this page and associated pages is to describe the classification used and to explain how these models can be generated; it does not provide a review of superposed folding and associated references. However, I refer to the literature that I used for creating these models which should give students unfamiliar with classification and computer programs of refolded folds a good starting point.
Please feel free to contact me if you have any suggestions of how to improve the script or if you think it would be very useful to add some other models!
Martin Schöpfer
Email: martin@fag.ucd.ie
Classification
Refold structures are typically divided, based on their 2D interference pattern, into four types (Type 0-3; Ramsay 1962, J. Geol. 70, 466-481). This nomenclature, which is widely used by structural geologists, has recently been extended to six types (Type 1-3 and Type 01-03; Grasemann et al. 2004, J. Geol. 112, 119-125). The figure below, kindly provided by Bernhard Grasemann, illustrates the extended classification scheme which is used to describe the papermodels provided here. In the extended classification Type 03 is identical to Type 0; Type 01 and Type 02 do not generate an interference pattern (hence they were excluded in the original classification), but do fold a lineation contained within the first fold. Perhaps most importantly various transitional forms can be better classified using the extended scheme and, although the end members Type 01 and 02 do not generate interference patterns, transitional forms (Type 01 ↔ 02) do.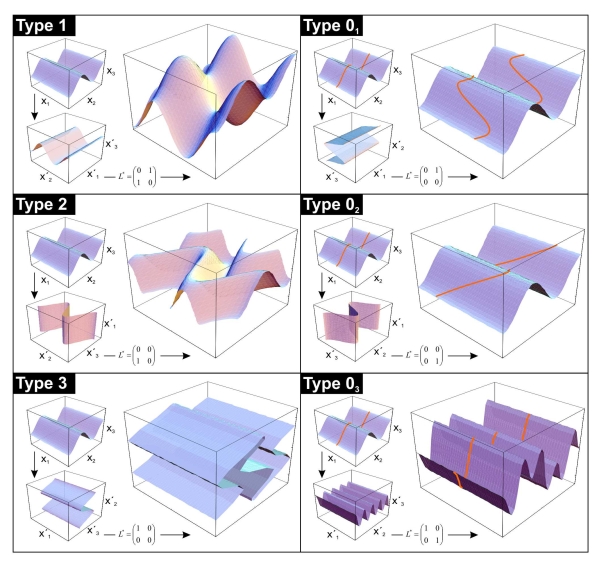
The reference axes of the folds shown in the figure above are:
x1 - fold axis
x2 - normal to the fold axial plane
x3 - shear direction in the axial plane
where the primed axes labels are the reference axes of the superposed folds.
Papermodels
The list below provides links to tables of superposed folding papermodels. Each low resolution papermodel image is a link to a high resolution PNG file which opens in a new window (alternatively you can use 'Save Target As...'). Surface plots, similar to those shown above, are provided which illustrate the 3D geometry of a central layer. A stereonet that shows the orientation of the first fold and the refold fold is also provided. Orientations of the two folds are given in terms of dip direction and dip of the fold axial planes, and pitch (rake) of the fold axes. In the papermodels the dip direction and dip of the first fold is always 000/90 with a rake of 0. Hence in the stereonets associated with each model, x1 and x2 in the figure above are horizontal and orientated E-W and N-S, respectively.Each papermodel also contains information about the amplitude and wavelength of the two fold systems. Folds are idealised using the following plane-strain equations (see p. 955 in: Ramsay and Lisle, 2000. The Techniques of Modern Structural Geology)
where x0, y0 and z0 are initial positions and xf, yf and zf the deformed (finite) co-ordinates. The fold amplitude is AB, and factors B and C are stretches (homogeneous strain). If C = 1/B deformation is constant volume. The great advantage of this set of equations is that it is also possible to superimpose homogenous strain by setting parameter A to zero.
Because there are six end-members and 15 possible intermediate types the papermodels are grouped using the same scheme as in Grasemann et al. (2004):
- End Members:
Six end members of refold structures are distinguished. The reference axes of the initial and the superposed folds are either perpendicular or parallel to each other. Type 01 and Type 02 do not generate interference patterns but are included in the table for completeness; the 01 and 02 models basically illustrate the geometry of the first fold.
- Intermediate Types - Parallel Rotation:
Nine intermediate types that can be obtained by rotation around one of the fold reference axes are possible. For example the intermediate Type 1 ↔ 2 is obtained by a rotation around x2 of the refold fold (see figure above). All the intermediate type papermodels available under the heading 'parallel rotation' are forms that were obtained by a rotation of 45o around the appropriate reference axis. Note that Type 01 ↔ 02 does not modify the first fold and that Type 02 ↔ 03 only leads to an increase in fold amplitude, but are included in the table for the sake of completeness.
- Intermediate Types - Oblique Rotation:
Six intermediate types that can be obtained by rotation around an axis which is oblique to the reference axes. The rotation axis makes an angle of 55o (more precisely cos-1(3-1/2)) with all three (mutually perpendicular) reference axes. A rotation of 120o around this axis leads to the transition from one reference axes orientation to the other (e.g. Type 1 ↔ 3). Because all end member papermodels have refold fold reference axes which are N-S, E-W and vertical, the plunge direction and plunge of (one possible) rotation axis is 045/35 (whether the rotation is clockwise or anti-clockwise depends on the transition). All the intermediate type papermodels available under the heading 'oblique rotation' are forms that were obtained by a rotation of 60o around this rotation axis.
Matlab script
All the papermodels available on this webpage were generated using a Matlab script. Because there are myriads of refolding folds (or homogenous strain superposition), I decided to provide only the end-members and the intermediate members exactly between the end members on this page. However, the script is easy to use and the various parameters can be changed easily. Hence students can experiment and design their own models.Instructions of how to use and modify the script can be found here.
The script and associated functions can be downloaded here.
________________________________________________________________
Last update: February 2009
Check out links on our website for Educational Material and photo Gallery.