Complete set of equations used for generating fold interference pattern

Below the full set of equations for superposed folding for two fold systems with any orientation is given. The main primary source for the equations outlined here is Session 36 (Heterogeneous Finite Strain: 4. Three-Dimensional Methods) in Ramsay and Lisle, 2000. The Techniques of Modern Structural Geology. Volume 3: Applications of Continuum Mechanics in Structural Geology. Academic Press., which is strongly recommended reading.

Folds are idealised using the following plane-strain equations:

$\; x$_f = x₀
  y_f = Cy₀
  z_f = ABsiny₀ + Bz₀

The fold amplitude is AB, and factors B and C are stretches (homogeneous strain). If C = 1/B deformation is constant volume. Subscripts 1 and 2 in the equations below denote the fold parameters of the 1st and 2nd set of folds.

The orientations of the folds are given by dip directions θ and dips δ of the fold axial planes, and by the pitches (or rakes) φ of the fold axes. The rotation angles used in the equations listed below are given by:

$\; \alpha$_x = 90^o - δ₁
  α_y = φ₁
  α_z = -θ₁

  β_x = 90^o - δ₂
  β_y = φ₂
  β_z = -θ₂

where subscripts 1 and 2 denote the orientations of the 1st and 2nd set of folds (the minus sign for the z-rotations is used because clockwise rotation in geology (e.g. stereonet) is positive and negative in mathematics).

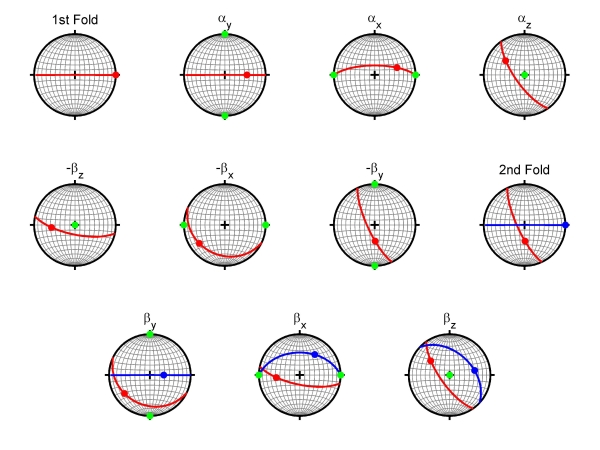
Because the fold equations result in folds that are upright, with horizontal fold axes, various rotations are required to take into account the different fold orientations. The different steps required for superposed folding are illustrated using stereonets in the diagram below using a Cartesian co-ordinate system where x is E-W, y is N-S and z is vertical. Rotation axes are shown in green, first fold in red and second fold in blue:

1. 1st folding.



2. Rotate 1st fold to its position (FAP₁ = 235/71 and φ₁ = -45 in the example shown) with rotations α_y, α_x and α_z.



3. Rotate 1st fold so that the 2nd fold orientation is FAP₂ = 000/90 and φ₂ = 0 using rotations -β_z, -β_x and -β_y.



4. 2nd folding.



5. Rotate both folds so that the 2nd fold is in its required position (FAP₂ = 043/44 and φ₂ = -62 in the example shown) with rotations β_y, β_x and β_z.

The steps described and illustrated above are Lagrangian, where finite (deformed) positions are expressed as functions of their original positions. These equations can be used, for example, to plot the folded surface in 3D. In order to construct an interference pattern, however, Eulerian forms are required that express the initial (undeformed) positions as a function of their finite (deformed) positions. The folding equation at the top of this page, for example, is written in its Eulerian form as:

$\; x$₀ = x_f
  y₀ = y_f/C
  z₀ = -(ABsin(y_f/C)-z_f)/B

Basically we need to determine for points that describe the surface where the interference pattern is observed (e.g. outcrop) where these points came from. If we know for each point where it came from, i.e. its initial position (x₀,y₀,z₀), then we can also determine from which layer it came from. If, for example, initial layering was horizontal, then we need to calculate z₀ for each point on the surface of observation and then colour points that have z₀-values within a given interval defined by the initial position of the upper and lower boundary of that layer.

The complete set of equations in their Eulerian form are:

β_z - rotation:

$\; x$₁ = x_fcosβ_z + y_fsinβ_z
  y₁ = -x_fsinβ_z + y_fcosβ_z
  z₁ = z_f

β_x - rotation:

$\; x$₂ = x₁
  y₂ = y₁cosβ_x + z₁sinβ_x
  z₂ = -y₁sinβ_x + z₁cosβ_x

β_y - rotation:

$\; x$₃ = x₂cosβ_y + z₂sinβ_y
  y₃ = y₂
  z₃ = -x₂sinβ_y + z₂cosβ_y

2nd fold, i.e. refold fold:

$\; x$₄ = x₃
  y₄ = y₃/C₂
  z₄ = -(A₂B₂sin(y₃/C₂)-z₃)/B₂

-β_y - rotation:

$\; x$₅ = x₄cosβ_y - z₄sinβ_y
  y₅ = y₄
  z₅ = x₄sinβ_y + z₄cosβ_y

-β_x - rotation:

$\; x$₆ = x₅
  y₆ = y₅cosβ_x - z₅sinβ_x
  z₆ = y₅sinβ_x + z₅cosβ_x

-β_z - rotation:

$\; x$₇ = x₆cosβ_z - y₆sinβ_z
  y₇ = x₆sinβ_z + y₆cosβ_z
  z₇ = z₆

α_z - rotation:

$\; x$₈ = x₇cosα_z + y₇sinα_z
  y₈ = -x₇sinα_z + y₇cosα_z
  z₈ = z₇

α_x - rotation:

$\; x$₉ = x₈
  y₉ = y₈cosα_x + z₈sinα_x
  z₉ = -y₈sinα_x + z₈cosα_x

α_y - rotation:

$\; x$₁₀ = x₉cosα_y + z₉sinα_y
  y₁₀ = y₉
  z₁₀ = -x₉sinα_y + z₉cosα_y

1st fold:

$\; x$₀ = x₁₀
  y₀ = y₁₀/C₁
  z₀ = -(A₁B₁sin(y₁₀/C₁)-z₁₀)/B₁

One can obtain an expression z₀ = f(x_f,y_f,z_f) by substituting the first set into the second, the second into the third and so on; the final equation is very long and used in the Matlab script.

BACK